Typesystem
Defining A Typesystem For Your Language
This page describes the MPS type-system to a great detail. If you would prefer a more lightweight introduction into defining your first type-system rules, consider checking out the Type-system cookbook.
If you would like to get familiar with the ways you can use the type-system from your code, you may also look at the Using the type-system chapter.
What is a typesystem?
A typesystem is a part of a language definition assigning types to the nodes in the models written using the language. The typesystem language is also used to check certain constraints on nodes and their types. Information about types of nodes is useful for:
finding type errors
checking conditions on nodes' types during generation to apply only appropriate generator rules
providing information required for certain refactorings (for example, for the "extract variable" refactoring)
and more
Types
To enable MPS to assign types to nodes of your language, you should create a language aspect for the typesystem. The typesystem model for your language will be written in the typesystem language.
Concepts for types
Types are defined as ordinary concepts in MPS. Expressions (nodes) indicate their types by instantiating the type concepts in the type inference rules, such as in typeof(thisNode) :==: new node<MyType> Some concepts carry the type information as their child, e.g. VariableDeclaration in BaseLanguage. Think of a type as a marker on a node that the typesystem assigns to it.
Types can be freely combined into bigger types (e.g. type parameters). Not all concepts, however, may serve as types. It is advisable to avoid children in type concepts that would not be types themselves. That is because the type-system, when comparing two types, compares their contents for equality and only if the match is perfect it treats the nodes as the same type. Types are also generally independent of the storage, whereas ordinary nodes belong to some model.
Some types do not need to hold any additional information. For example, the IntegerType in BaseLanguage is just an indicator that an expression represents a value of a numeric value - int a = 5;
Some types may need to hold properties, children or references to other nodes, like e.g. ClassifierType in BaseLanguage, which represents a type defined by a class:
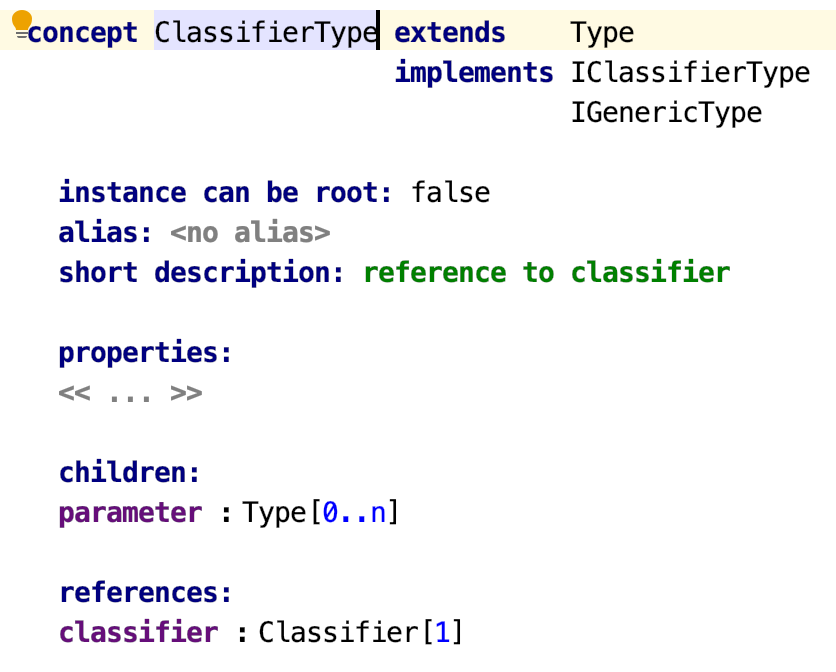
Effectively the ClassifierType is a term (node) that serves as an assertion that an expression typed with it, after it is evaluated, is an instance of that class.
Inference Rules
The main concept of the typesystem language is an inference rule. An inference rule for a certain concept is mainly responsible for computing a type for instances of that concept.
An inference rule consists of a condition and a body. A condition is used to determine whether a rule is applicable to a certain node. A condition may be of two kinds: a concept reference or a pattern. A rule with a condition in the form of concept reference is applicable to every instance of that concept and its subconcepts. A rule with a pattern is applicable to nodes that match the pattern. A node matches a pattern if it has the same properties and references as the pattern, and if its children match the pattern's children. A pattern also may contain several variables which match everything.
The body of an inference rule is a list of statements which are executed when a rule is applied to a node. The main kind of statements of typesystem language are statements used for creating equations and inequations between types.
An inference rule may define the overrides block, which is a boolean flag that tells the typechecker that, in case there are other inference rules applicable to the superconcepts of the concept specified in the condition, this inference rule takes precedence, and all the rules for superconcepts are ignored. The version 3.3 brings possibility to use a code block instead of a static flag. Version 2021.3.3 introduces two new options:
An inference rule can be defined in an extending language and be applicable to a concept from the extended language.
The overrides flag works for such inference rules in the extending language - it causes the rule to override all the rules defined for the superconcepts as well as the rules defined in the extended language for the particular concept.
it also covers situations where inference rules are defined for the same concept in languages that are being extended, in which case these original rules are also ignored.
The inference rules that are applicable to instances of node attributes have additional features that allow for amending the rules applied to the attributed node. These can either be applied together with the attributed node’s inference rules or supersede them altogether. This, for example, can be used to implement alternate type inference based on presence conditions, which can take into account the parameters specified at the project or system level.
In case an inference rule is applicable to a node attribute, there is also a possibility to tell the typechecker that this rule supercedes the rules applicable to the attributed node, which are then ignored. Also, the attributed node is accessible in all rule's code blocks as attributedNode.
Inference Methods
To avoid duplications, one may want to extract identical parts of code of several inference rules to a method. An inference method is just a simple Base Language method marked with an annotation "@InferenceMethod". There are several language constructions you may use only inside inference rules and replacement rules and inference methods, they are: typeof expressions, equations and inequations, when concrete statements, type variable declarations and type variable references, and invocations of inference methods. That is made for not to use such constructions in arbitrary methods, which may be called in arbitrary context, maybe not during type checking.
Equations And Inequations
The main process which is performed by the type-system engine is the process of solving equations and inequations among all the types. A language designer tells the engine, which equations it should solve by writing them in inference rules. To add an equation into an engine, the following statement is used:
expr1 :==: expr2 where expr1 and expr2 are expressions, which evaluate to a node.
Consider the following use case. You want to say that the type of a local variable reference is equal to the type of the variable declaration it points to. So, you write typeof (varRef) :==: typeof (varRef.localVariableDeclaration), and that's all. The typesystem engine will solve such equations automatically.
The above-mentioned expression typeof(expr) (where expr must evaluate to an MPS node) is a language construct, which returns a so-called type variable, which serves as a type of that node. Type variables become concrete types gradually during the process of equation solving.
In certain situations you want to say that a certain type doesn't have to exactly equal another type, but also may be a subtype or a supertype of that type. For instance, the type of the actual parameter of a method call does not necessarily have to be the same type as that of the method's formal parameter - it can be its subtype. For example, a method, which requires an Object as a parameter, may be applied also to a String.
To express such a constraint, you may use an inequation instead of an equation. An inequation expresses the fact that a certain type should be a subtype of another type. It is written as follows: expr1 :<=: expr2
Weak And Strong Subtyping
A relationship of subtyping is useful for several different cases. You want a type of an actual parameter to be a subtype of formal parameter type, or you want a type of an assigned value to be a subtype of variable's declared type; in method calls or field access operations you want a type of an operand to be a subtype of a method's declaring class.
Sometimes such demands are somewhat controversial: consider, for instance, two types, int and Integer, which you want to be interchangeable when you pass parameters of such types to a method: if a method is doSomething(int i), it is legal to call doSomething(1) as well as doSomething(new Integer(1)). But when these types are used as types for operand of, say, a method call, the situation is the different: you shouldn't be able to call a method of an expression of type int, of an integer constant for example. So, we have to conclude that in one sense int and Integer are subtypes of one another, while in the other sense they are not.
For solving such a controversy, we introduce two relationships of subtyping: namely, weak and strong subtyping. Weak subtyping will follow from strong subtyping: if a node is a strong subtype of another node, then it is it's weak subtype also.
Then, we can say about our example, that int and Integer are weak subtypes of each other, but they are not strong subtypes. Assignment and parameters passing require weak subtyping only, method calls require strong subtyping.
When you create an inequation in you typesystem, you may choose it to be a strong or weak inequation. Also subtyping rules, those which state subtyping relationship (see below), can be either weak or strong. A weak inequation looks like :<=:, a strong inequation looks like :<<=:
In most cases you want to state strong subtyping, and to check weak subtyping. If you are not sure, which subtyping you need, use weak one for inequations, strong one for subtyping rules.
Subtyping Rules
When the typesystem engine solves inequations, it requires information about whether a type is a subtype of another type. But how does the typesystem engine know about that? It uses subtyping rules. Subtyping rules are used to express subtyping relationship between types. In fact, a subtyping rule is a function which, given a type, returns its immediate supertypes.
A subtyping rule consists of a condition (which can be either a concept reference or a pattern) and a body, which is a list of statements that compute and return a node or a list of nodes that are immediate supertypes of the given node. When checking whether some type A is a supertype of another type B, the typesystem engine applies subtyping rules to B and computes its immediate supertypes, then applies subtyping rules to those supertypes and so on. If type A is among the computed supertypes of type B, the answer is "yes".
By default, subtyping stated by subtyping rules is a strong one. If you want to state only weak subtyping, set "is weak" property of a rule to "true".
Comparison Inequations And Comparison Rules
Consider you want to write a rule for EqualsExpression (operator == in Java, BaseLanguage and some other languages): you want left operand and right operand of EqualsExpression to be comparable, that is either type of a left operand should be a (non-strict) subtype of a right operand, or vice versa. To express this, you write a comparison inequation, in a form expr1 :~: expr2, where expr1 and expr2 are expressions, which represent types. Such an inequation is fulfilled if expr1 is a subtype of expr2
or
Then, consider that, say, any Java interfaces should also be comparable, even if such interfaces are not subtypes of one another. That is because there always can be written a class, which implements both of interfaces, so variables of interface types can contain the same node, and variable of an interface type can be cast to any other interface. hence an equation, cast, or instanceof expressions with both types being interface types should be legal (and, for example, in Java they are).
To state such a comparability, which does not stem from subtyping relationships, you should use comparison rules. A comparison rule consists of two conditions for the two applicable types and a body which returns true if the types are comparable or false if they are not.
Here's the comparison rule for interface types:
comparison rule interfaces_are_comparable
Quotations
A quotation is a language construct that lets you easily create a node with a required structure. Of course, you can create a node using the smodelLanguage and then populate it with appropriate children, properties and references by hand, using the same smodelLanguage. However, there's a simpler - and more visual - way to accomplish this.
A quotation is an expression, whose value is the MPS node written inside the quotation. Think about a quotation as a "node literal", a construction similar to numeric constants and string literals. That is, you write a literal if you statically know what value do you mean. So inside a quotation you don't write an expression, which evaluates to a node, you rather write the node itself. For instance, an expression 2 + 3 evaluates to 5, an expression < 2 + 3 > (angled braces being quotation braces) evaluates to a node PlusExpression with leftOperand being an IntegerConstant 3 and rightOperand being IntegerConstant 5.
(See the Quotations documentation for more details on quotations, anti quotations and light quotations)
Antiquotations
For it is a literal, a value of quotation should be known statically. On the other hand, in cases when you know some parts (i.e. children, referents or properties) of your node only dynamically, i.e. those parts that can only be evaluated at runtime and are not known at design time, then you can't use just a quotation to create a node with such parts.
The good news, however, is that if you know the most part of a node statically and you want to replace only several parts by dynamically-evaluated nodes you can use antiquotations. An antiquotation can be of 4 types: child, reference, property and list antiquotation. They all contain an expression, which evaluates dynamically to replace a part of the quoted node by its result. Child and referent antiquotations evaluate to a node, property antiquotation evaluates to string and list antiquotation evaluates to a list of nodes.
For instance, you want to create a ClassifierType with the class ArrayList, but its type parameter is known only dynamically, for instance by calling a method, say, "computeMyTypeParameter()".
Thus, you write the following expression: < ArrayList < %( computeMyTypeParameter() )% > >. The construction %(...)% here is a node antiquotation.
You may also antiquotate reference targets and property values, with ^(...)^ and $(...)$, respectively; or a list of children of one role, using *(...)*.
a) If you want to replace a node somewhere inside a quoted node with a node evaluated by an expression, you use node antiquotation, that is %( )%. As you may guess there's no sense to replace the whole quoted node with an antiquotation with an expression inside, because in such cases you could instead write such an expression directly in your program.
So node antiquotations are used to replace children, grandchildren, great-grandchildren and other descendants of a quoted node. Thus, an expression inside of antiquotation should return a node. To write such an antiquotation, place the caret in a cell for a child and type "%".
b) If you want to replace a target of a reference from somewhere inside a quoted node with a node evaluated by an expression, you use reference antiquotation, that is ^(...)^ . To write such an antiquotation, place the caret in a cell for a referent and type "^".
c) If you want to replace a child (or some more deeply located descendant), which is of a multiple-cardinality role, and if for that reason you may want to replace it not with a single node but rather with several ones, then use child list (simply list for brevity) antiquotations, *( )* .An expression inside a list antiquotation should return a list of nodes, that is of type nlist<..> or compatible type (i.e. list<node<..>> is ok, too, as well as some others). To write such an antiquotation, place the caret in a cell for a child inside a child collection and type "*" . You cannot use it on an empty child collection, so before you press "*" you have to enter a single child inside it.
d) If you want to replace a property value of a quoted node by a dynamically calculated value, use property antiquotation $( )$. An expression inside a quotation should return string, which will be a value for an antiquoted property of a quoted node. To write such an antiquotation, place the caret in a cell for a property and type "$".
(See the Quotations documentation for more details on quotations, anti quotations and light quotations)
Examples Of Inference Rules
Here are the simplest basic use cases of an inference rule:
to assign the same type to all instances of a concept (useful mainly for literals):
applicable to concept = StringLiteral as nodeToCheck { typeof (nodeToCheck) :==: <String> }to equate a type of a declaration and the references to it (for example, for variables and their usages):
applicable to concept = VariableReference as nodeToCheck { typeof (nodeToCheck) :==: typeof (nodeToCheck.variableDeclaration) }to give a type to a node with a type annotation (for example, type of a variable declaration):
applicable to concept = VariableDeclaration as nodeToCheck { typeof (nodeToCheck) :==: nodeToCheck.type }to establish a restriction for a type of a certain node: useful for actual parameters of a method, an initializer of a type variable, the right-hand part of an assignment, etc.
applicable to concept = AssignmentExpression as nodeToCheck { typeof (nodeToCheck.rValue) :<=: typeof (nodeToCheck.lValue) }
Type Variables
Inside the typesystem engine during type evaluation, a type may be either a concrete type (a node) or a so-called type variable. Also, it may be a node which contains some type variables as its children or further descendants. A type variable represents an undefined type, which may then become a concrete type, as a result of solving equations that contain this type variable.
Type variables appear at runtime mainly as a result of the "typeof" operation, but you can create them manually, if you want to. There's a statement called TypeVarDeclaration in the typesystem lanuage to do so. You write it like "var T" or "var X" or "var V", i.e. "var" followed by the name of a type variable. Then you may use your variable, for example, in antiquotations to create a node with type variables inside.
Example: an inference rule for "for each" loop. A "for each" loop in Java consists of a loop body, an iterable to iterate over, and a variable into which the next member of an iterable is assigned before the next iteration. An iterable should be either an instance of a subclass of the Iterable interface, or an array. To simplify the example, we don't consider the case of the iterable being an array. Therefore, we need to express the following: an iterable's type should be a subtype of an Iterable of something, and the variable's type should be a supertype of that very something. For instance, you can write the following:
or the following:
Iterables in both examples above have the type ArrayList<String>, which is a subtype of Iterable<String>. Variables have types String and Object, respectively, both of which are subtypes of String.
As we see, an iterable's type should be a subtype of an Iterable of something, and the variable's type should be a supertype of that very something. But how to say "that very something" in the typesystem language? The answer is, it's a type variable that we use to express the link between the type of an iterable and the type of a variable. So we write the following inference rule:
Meet and Join types
Meet and Join types are special types, which are treated differently by the typesystem engine. Technically Meet and Join types are instances of MeetType and JoinType concepts, respectively. They may have an arbitrary number of argument types, which could be any nodes. Semantically, a Join type is a type, which is a supertype of all its arguments, and a node which has a type Join(T1|T2|..Tn) can be regarded as if it had type T1 or type T2 or... or type Tn. A Meet type is a type, which is a subtype of its every argument, so one can say that a node, which has a type Meet(T1&T2&..&Tn) inhabits type T1 and type T2 and.. and type Tn. The separators of arguments of the Join and Meet types (i.e. "|" and "&") are chosen respectively to serve as a mnemonics.
Meet and Join types are very useful at certain situations. Meet types appear even in MPS BaseLanguage (which is very close to Java). For instance, the type of such an expression:
is Meet(Serializable & Comparable), because both Integer (the type of new Integer(1)) and String (the type of "hello") implement both Serializable and Comparable.
Join type is useful when, say, you want some function-like concept return values of two different types (node or list of nodes, for instance). Then you should make type of its invocation be Join(node<> | list<node<>>).
You can create Meet and Join types by yourself, if you need to. Use quotations to create them, just as with other types and other nodes. The concepts of Meet and Join types are MeetType and JoinType, as it is said above.
"When Concrete" Blocks
Sometimes you may want not only to write equations and inequations for a certain types, but to perform some complex analysis with type structure. That is, inspect inner structure of a concrete type: its children, children of children, referents, etc.
It may seem that one just may write typeof(some expression), and then analyze this type. The problem is, however, that one can't just inspect a result of "typeof" expression because it may be a type variable at that moment. Although a type variable usually will become a concrete type at some moment, it can't be guaranteed that it is concrete in some given point of your typesystem code.
To solve such a problem you can use a "when concrete" block.
Here, "expr" is an expression which will evaluate to a mere type you want to inspect (not to a node type of which you want to inspect), and "var" is a variable to which an expression will be assigned. Then this variable may be used inside a body of "when concrete" block. A body is a list of statements which will be executed only when a type denoted by "expr" becomes concrete, thus inside the body of a when concrete block you may safely inspect its children, properties, etc. if you need to.
If you have written a when concrete block and look into its inspector you will see two options: "is shallow" and "skip error". If you set "is shallow" to "true", the body of your when concrete block will be executed when expression becomes shallowly concrete, i.e. becomes not a type variable itself but possibly has type variables as children or referents. Normally, if your expression in condition of when concrete block is never concrete, then an error is reported. If it is normal for a type denoted by your expression to never become a concrete type, you can disable such error reporting by setting "skip error" to true.
Overloaded Operators
Sometimes an operator (like +, -, etc.) has different semantics when applied to different values. For example, + in Java means addition when applied to numbers, and it means string concatenation if one of its operands is of type String. When the semantics of an operator depends on the types of its operands, it's called operator overloading. In fact, we have many different operators denoted by the same syntactic construction.
Let's try to write an inference rule for a plus expression. First, we should inspect the types of operands, because if we don't know the types of operands (whether they are numbers or Strings), we cannot choose the type for an operation (it will be either a number or a String). To be sure that types of operands are concrete we'll surround our code with two when concrete blocks, one for left operand's type and another one for right operand's type.
}
Then, we can write some inspections, where we check whether our types are strings or numbers and choose an appropriate type of operation. But there will be a problem here: if someone writes an extension of BaseLanguage, where they want to use the plus expression for addition of some other entities, say, matrices or dates, they won't be able to use plus expression because types for plus expression are hard-coded in the already existing inference rule. So, we need an extension point to allow language-developers to overload existing binary operations.
Typesystem language has such an extension point. It consists of:
overloading operation rules and
a construct which provides a type of operation by operation and types of its operands.
For instance, a rule for PlusExpression in BaseLanguage is written as follows:
Here, "operation type" is a construct which provides a type of an operation according to types of operation's left operand's type, right operand's type and the operation itself. For such a purpose it uses overloading operation rules.
Overloaded Operation Rules
Overloaded operation rules reside within a root node of concept OverloadedOpRulesContainer. Each overloaded operation rule consists of:
an applicable operation concept, i.e. a reference to a concept of operation to which a rule is applicable (e.g. PlusExpression);
left and right operand type restrictions, which contain a type which restricts a type of left/right operand, respectively. A restriction can be either exact or not, which means that a type of an operand should be exactly a type in a restriction (if the restriction is exact), or its subtype (if not exact), for a rule to be applicable to such operand types;
a function itself, which returns a type of the operation knowing the operation concept and the left and right operand types.
Here's an example of one of overloading operation rules for PlusExpression in BaseLanguage:
Replacement Rules
Motivation
Consider the following use case: you have types for functions in your language, e.g. (a 1, a 2 ,...a N) -> r, where a 1, a 2, .., a N, and r are types: a K is a type of K-th function argument and r is a type of a result of a function. Then you want to say that your function types are covariant by their return types and contravariant by their argument types. That is, a function type F = (T 1, .., T N) -> R is a subtype of a function type G = (S 1, .., S N) -> Q (written as F <: G) if and only if R <: Q (covariant by return type) and for any K from 1 to N, T K :> S K (that is, contravariant by arguments types).
The problem is, how to express covariance and contravariance in the typesystem language? Using subtyping rules you may express covariance by writing something like this:
Okay, we have collected all immediate supertypes for a function's return type and have created a list of function types with those collected types as return types and with original argument types. But, first, if we have many supertypes of return type, it's not very efficient to perform such an action each time we need to solve an inequation, and second, although now we have covariance by function's return type, we still don't have contravariance by function's arguments' types. We can't collect immediate subtypes of a certain type because subtyping rules give us supertypes, not subtypes.
In fact, we just want to express the abovementioned property: F = (T 1, .., T N) -> R <: G = (S 1, .., S N) -> Q (written as F <: G) if and only if R <: Q and for any K from 1 to N, T K :> S K. For this and similar purposes the typesystem language has a notion called "replacement rule."
A replacement rule can be overridden by another, more specific replacement rule defined in the same language or one of the extending languages. In case there are two candidate replacement rules that can be applied for a given pair of left and right types, the one that is specified with a more specific concept, either for the left or right type, wins.
Additionally, in case two or more rules are matching and all specify exactly same concepts, the one defined in a more specific language wins. The "overrides" condition is checked before a rule is selected for a particular combination of right and left concepts, and is defined to be false by default. If true, all rules that correspond to less specific matching conditions are eliminated from the applicability scope.
What's a replacement rule?
A replacement rule provides a convenient way to solve inequations. While the standard way is to transitively apply subtyping rules to a should-be-subtype until a should-be-supertype is found among the results (or is never found among the results), a replacement rule, if applicable to an inequation, removes the inequation and then executes its body (which usually contains "create equation" and "create inequation" statements).
Applicability of a replacement rule is decided based on:
The applicable for section, then defines the matching sub-typing relationship between two concepts.
The custom condition section, which is a boolean function calculating applicability arbitrarily from the two processed types.
The overrides flag, which alows a rule to override a rule defined for a sub-concept. If true, all rules that correspond to less specific matching conditions are eliminated from the applicability scope.
Examples
A replacement rule for above-mentioned example is written as follows:
Here we say that a rule is applicable to a should-be-subtype of concept FunctionType and a should-be-supertype of concept FunctionType. The body of a rule ensures that the number of parameter types of function types are equal, otherwise it reports an error and returns. If the numbers of parameter types of both function types are equal, a rule creates an inequation with return types and appropriate inequation for appropriate parameter types.
Another simple example of replacement rules usage is a rule, which states that a Null type (a type of null literal) is a subtype of every type except primitive ones. Of course, we can't write a subtyping rule for Null type, which returns a list of all types. Instead, we write the following replacement rule:
This rule is applicable to any should-be-supertype and to those should-be-subtypes which are Null types. The only thing this rule does is checking whether should-be-supertype is an instance of PrimitiveType concept. If it is, the rule reports an error. If is not, the rule does nothing, therefore the inequation to solve is simply removed from the typesystem engine with no further effects.
Different semantics
A semantic of a replacement rule, as explained above, is to replace an inequation with some other equations and inequations or to perform some other actions when applied. This semantic really doesn't state that a certain type is a subtype of another type under some conditions. It just defines how to solve an inequation with those two types.
For example, suppose that during generation you need to inspect whether some statically unknown type is a subtype of String. What will an engine answer when a type to inspect is Null type? When we have an inequation, a replacement rule can say that it is true, but for this case its abovementioned semantics is unuseful: we have no inequations, we have a question to answer yes or no. With function types, it is worse because a rule says that we should create some inequations. So, what do we have to do with them in our use case?
To make replacement rules usable when we want to inspect whether a type is a subtype of another type, a different semantic is given to replacement rules in such a case.
This semantic is as follows: each "add equation" statement is treated as an inspection of whether two nodes match; each "add inequation" statement is treated as an inspection of whether one node is a subtype of another; each report error statement is treated as "return false."
Consider the above replacement rule for function types:
In a different semantic, it will be treated as follows:
So, as we can see, the other semantic is quite an intuitive mapping between creating equations/inequations and performing inspections.
Type-system, trace
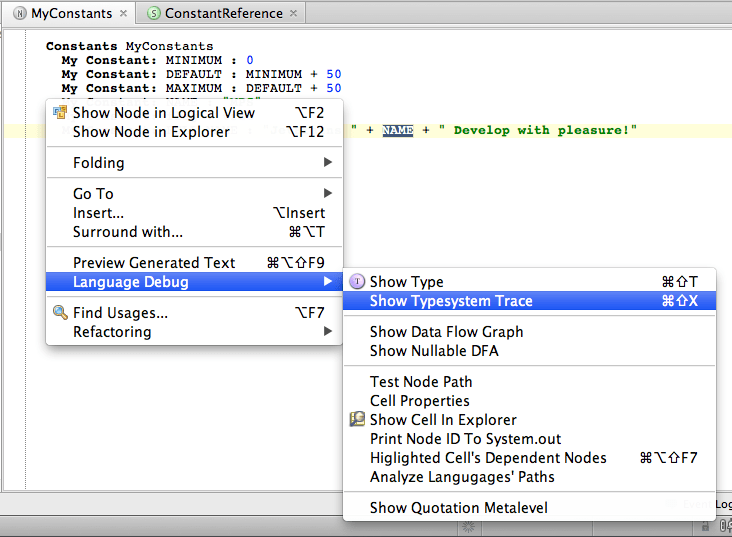
MPS provides a handy debugging tool that gives you insight into how the type-system engine evaluates the type-system rules on a particular problem and calculates the types. You invoke it from the context menu or by a keyboard shortcut Control/Cmd + Shift + X:
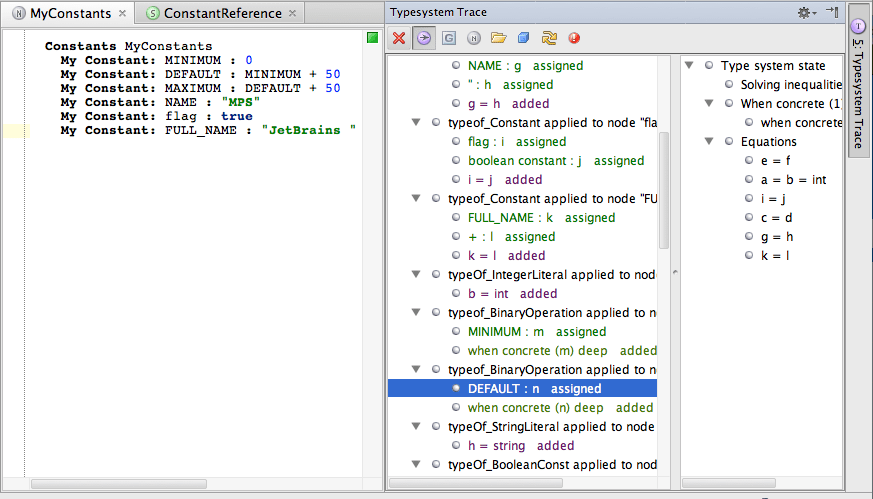
The console has two panels. The one on the left shows the sequence or rules as they were applied, while the one on the right gives you a snapshot of the type-system engine's working memory at the time of evaluating the rule selected in the left panel:
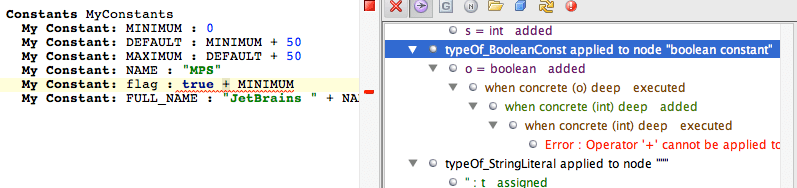
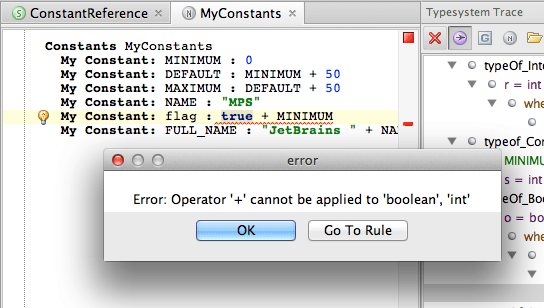
Type errors are marked inside the Type-system Trace panel with red color:
Additionally, if you spot an error in your code, use Control + Alt + Click / Cmd + Alt + Click to navigate quickly to the rule that fails to validate the types:
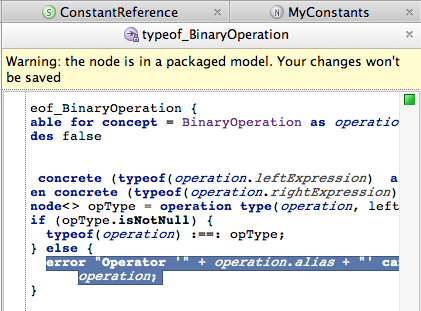
Advanced features of typesystem language
Substituting default type node
When type is assigned to a program node as a result of either applying an equation or resolving an inequality, the node to represent type is taken as is by default. That is to say, it may be a node in the program or be created with a quotation. In both cases, the result of evaluating the expression that specifies type to be assigned by either equation or inequality statement, literally represents target type. This feature allows to substitute another node to represent type instead.
For example, one might decide to use different types for different program configurations, such as using int or long depending on whether the task requires using one type or another. This is different from simply using the generator to produce the correct "implementation" type, as the substitution is done at the time the typechecking is performed, so possible errors can be caught early.
In its simplest form the type substitution can be used by creating an instance of Substitute Type Rule in the typesystem model.
The Substitute Type Rule is applicable to nodes that represent types. Whenever a new type is introduced by the typechecker, it searches for applicable substitution rules and executes them. The rule must either return an instance of `node<>` as the substitution, or null value, in which case the original node is used to represent the type (the default behaviour).
One other possibility to overrides types used by the typechecker comes with the use of node attributes. If there is a node attribute contained by the original type node, the typechecker tries to find a Substitute Type Rule applicable to the attribute first. This way one can override the type nodes even for languages, which implementation is sealed.
The rule above is defined for the attribute node, and it's the attribute node that is passed to the rule as the explicit parameter. The rule can check whether the condition for substituting the type node is satisfied, and it can also access the attributed node representing original type via attributedNode expression.
One caveat that should be mentioned, concerns the case when a type node just returned from a substitute rule, is itself a subject to another substitution. The typechecker tries to apply all matching substitution rules exhaustively, until no more substitutions are available. Only then the type appears in the internal model of the typechecker. Some precautions are taken to prevent the typechecker from going into an endless cycle of substitutions, such as A -> B -> A, but these are not perfect and one should be careful so as to not to introduce infinite cycles.
Check-only inequations
Basically, inequations may affect nodes' types, for instance if one of the inequation part is a type variable, it may become a concrete type because of this inequation. But, sometimes one does not want a certain inequation to create types, only to check whether such an inequation is satisfied. We call such inequations check-only inequations. To mark an inequation as a check-only, one should go to this inequation's inspector and should set a flag "check-only" to "true". To visually distinguish such inequations, the "less or equals" sign for check-only inequation is gray, while for normal ones it is black, so you can see whether an inequation is check-only without looking at its inspector.
Dependencies
When writing a generator for a certain language (see generator), one may want to ask for a type of a certain node in generator queries. When generator generates a model, such a query will make typesystem engine do some typechecking to find out the type needed. Performing full typechecking of a node's containing root to obtain the node's type is expensive and almost always unnecessary. In most cases, the typechecker should check only the node given. In more difficult cases, obtaining the type of a given node may require checking its parent or maybe a further ancestor. The typechecking engine will check a given node if the computed type is not fully concrete (i.e. contains one or more type variables); then the typechecker will check the node's parent, and so on.
Sometimes there's an even more complex case: the type of a certain node being computed in isolation is fully concrete; and the type of the same node - in a certain environment - is fully concrete also, but differs from the first one. In such a case, the abovementioned algorithm will break, returning the type of an node as if being isolated, which is not the correct type for the given node.
To solve this kind of problem, you can give some hints to the typechecker. Such hints are called dependencies - they express a fact that a node's type depends on some other node. Thus, when computing a type of a certain node during generation, if this node has some dependencies they will be checked also, so the node will be type-checked in an appropriate environment. A dependency is expressed by using the typeOf expression on the node, the type of which is needed for proper computation of the requested type.
Overriding type of literal or expression
In addition to type substitution rules, which are only applicable to types, we introduce support for attributes in the inference rules.
Inference rules
Literals or expressions usually have associated type inference rules that get triggered when the typechecker requires type of the node in question. The rules have a mechanism allowing subconcepts to extend or override the predefined rule.
Inference rules for node attributes
If a node has one or more attributes, the inference rules applicable to these attributes are applied before the rules applicable to the node itself. The process of applying inference rules can be described with a pseudo code.
An example of using an inference rule applicable to a node attribute shows how the presence condition can alter the type of a literal. Note that in this example the type of the annotated literal is affected by by both this inference rule and any other inference rule applicable to the node.
Conditionally overriding type inference
Keeping in mind that the condition under which the user might want to override the type inference via attributes depend on the configuration, we dont always want to override the default type.
Checking rules
Checking, (or Non-typesystem) rules can inspect the model searching for known error patterns in code and report them to the user. This kind of pre-compilation code inspection is generally known as static code analysis. Error patterns in typical tools for static code analysis can fall into several categories, such as correctness problems, multi-threaded correctness, I18N problems, vulnerability-increasing errors, styling issues, performance problems, etc. The found issues are reported to the user either on-demand through an interactive report:
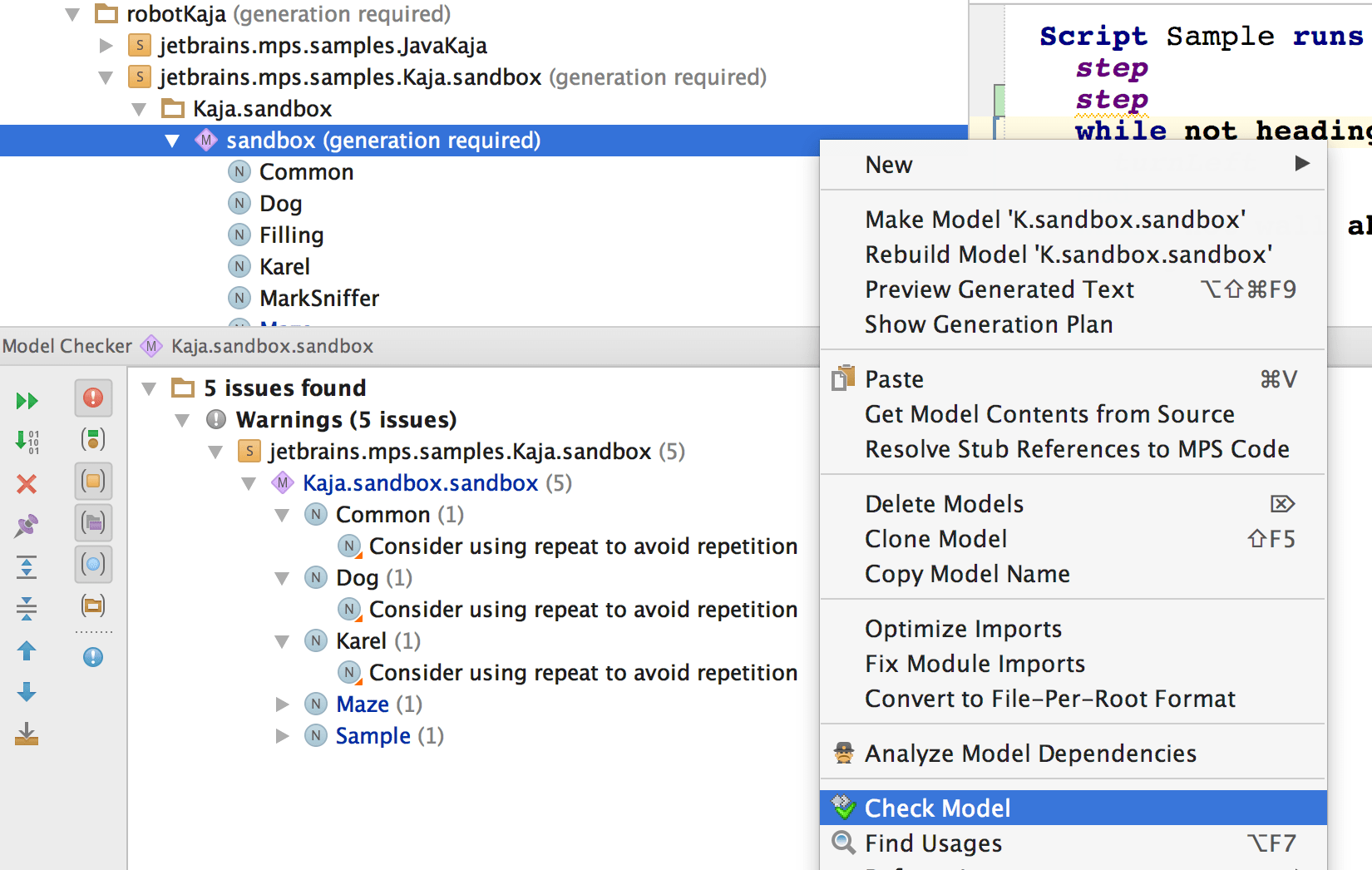
or in a on-the-fly mode directly in the editor by colorful symbols and code underlines:

Severity
MPS distinguishes problems by severity:
errors - displayed in red
warnings - displayed in yellow
infos - displayed in grayish
The jetbrains.mps.lang.typesystem language offers corresponding statements that emit these problem categories together with their description and the node to highlight. The additional ensure statement gives the user a more succinct syntax to report an error in case a condition is not met:
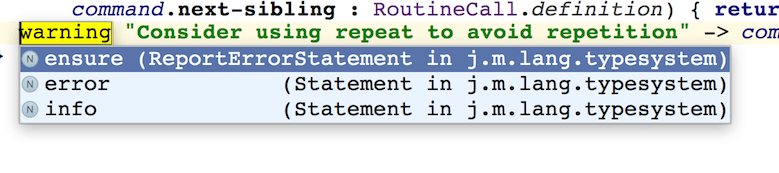
Checking rules typically check for one or a few related issues in a given node or a small part of the model and report to the user, if a problem is discovered. The checking rules are attached to a concrete concept:

The rule is called for every node that is an instance of that concept.
The applicability of a rule can be restricted to a specified pattern using the pattern language. This is handy for two main reasons:
narrowing the applicability condition of the rule to only some occurrences of the concept
convenient naming of properties, children, grandchildren of the node
Both goals can be achieved by using the pattern language inside a rule's body, in particular, using the match statement:

The pattern may contain variable parts (nodes, properties or references) that will match with any value, node or a reference in the model and the user can refer to them using the variable name.
The overrides option of a checking rule defines whether the current rule overrides some other checking rule that is applicable to a node.

A checking rule defined for some concept is by default inherited by all of its subconcepts. Checking a node thus includes executing all rules defined for the concept of the node as well as rules defined for its superconcepts. In the rather rare situations when such inheritance of checking rules ahould be avoided, the overrides option provides the means to do so. It enables you to explicitly specify the list of rules you want to override.
Alternatively, the option "extended" exists to override all rules applicable to the same concept and its super concepts from the languages being extended.
Multiple overridden rules can be selected:

Pattern language
The pattern language gives the user reasonable flexibility to specify the desired pattern. Using Intentions various parts of the pattern can be annotated with pattern-specific attributes and thus be given special meaning:
pattern variable - can be used to turn a node or a reference of the pattern into a variable. It will match with any value on the given position and the user will be able to obtain the value by referring to the pattern variable
pattern property variable - the same as above, but applied to properties of nodes
list pattern - will match with a collection of nodes and allow the user to iterate over them
or pattern - will match with one of several provided sub-patterns
wildcard - will match with any (even non-existent) node on a given position. The user cannot refer to the matched value
A match statement can be used to invoke node matching from BaseLanguage code:

Quick-fixes
A quick-fix provides a single model-transforming function, which will automatically eliminate the reported problem:
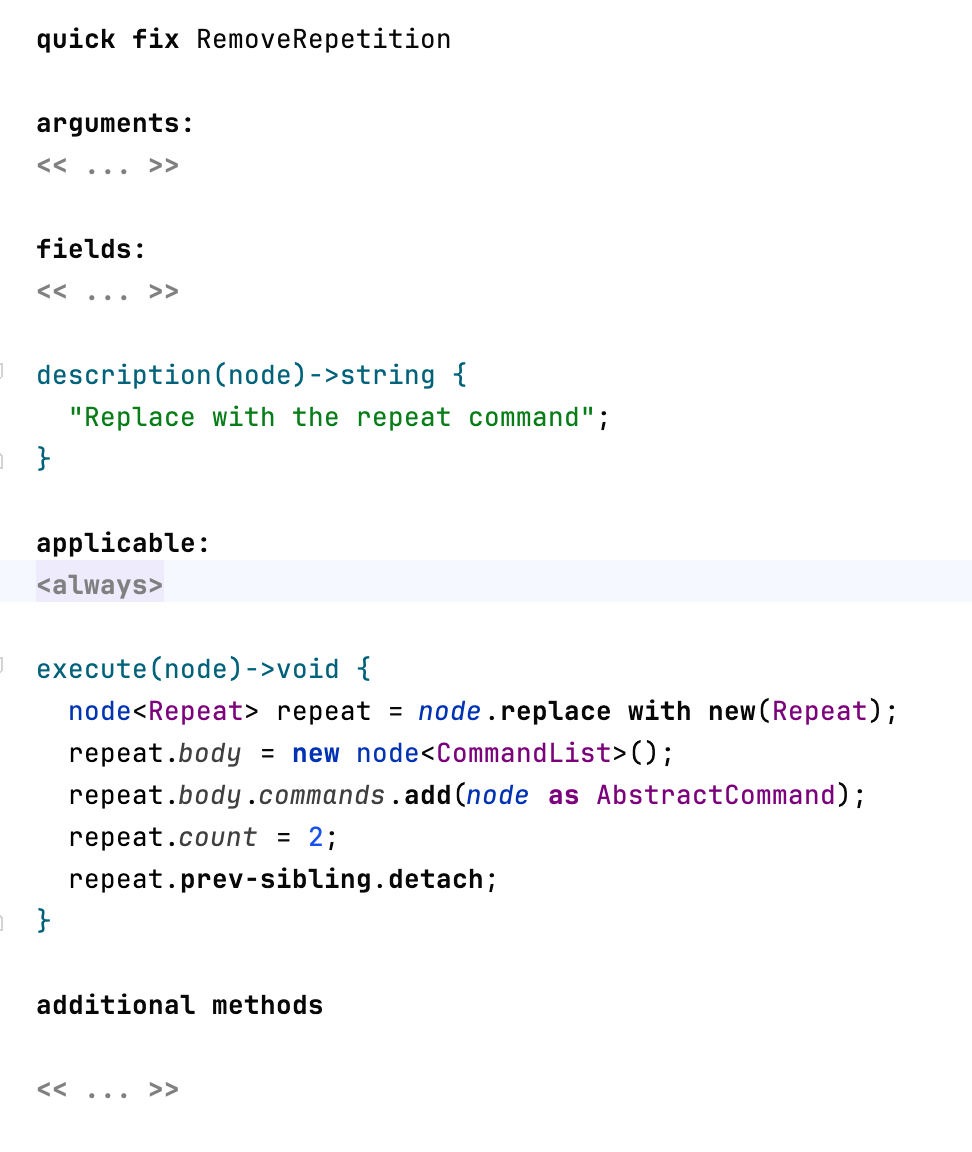
A quick-fix must provide a description to represent it in the Intentions context menu, unless it is only ever referred to from callers with apply immediately set to true. A quick-fix may also declare fields, to hold reused values, and it can accept arguments from the caller. The applicable function controls the applicability of the quick-fix, the default value <always> guarantees unrestricted applicability.
Invoking quick-fixes
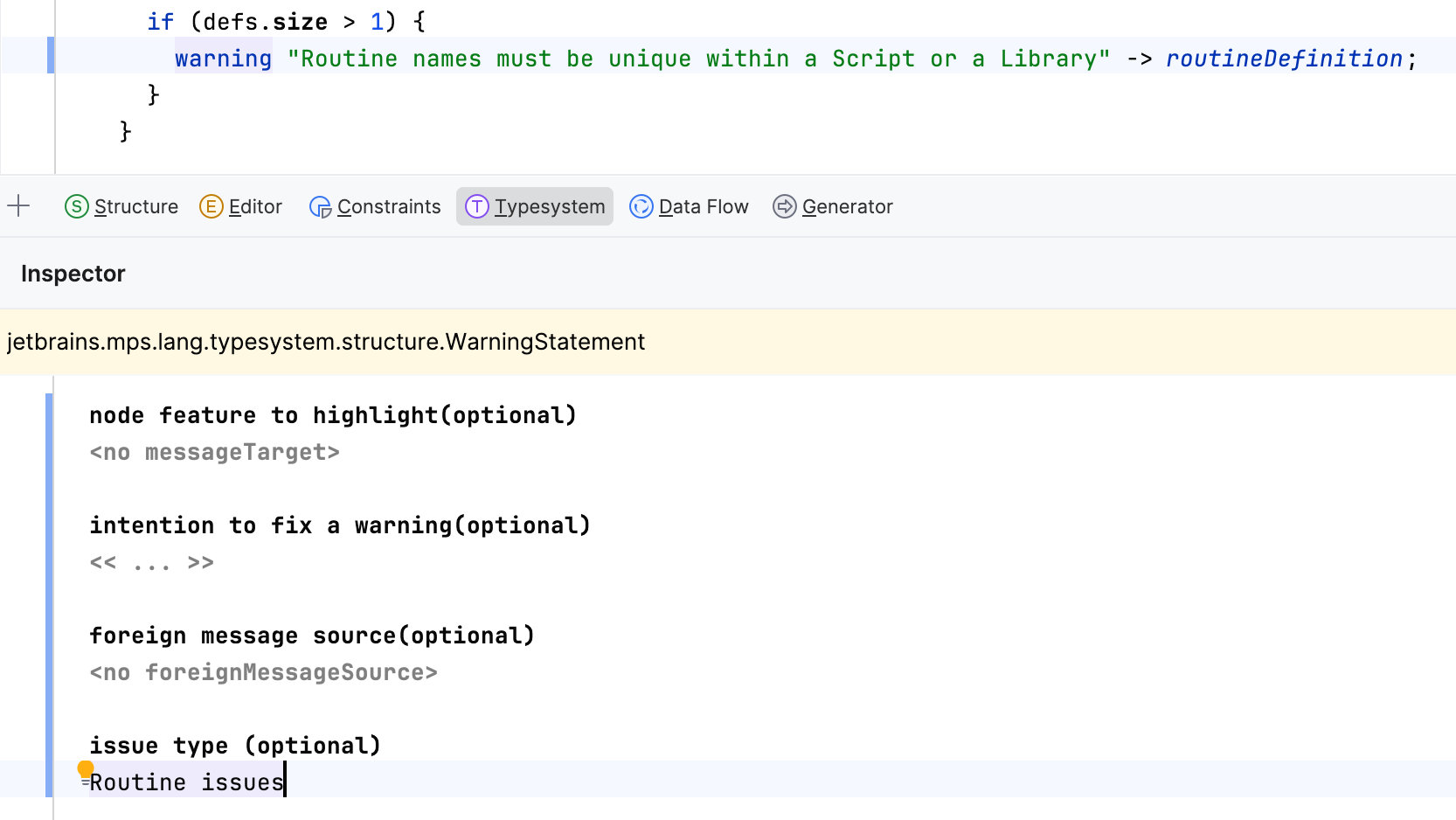
A quick-fix may be associated with each reported problem through the Inspector tool window using the intention to fix:
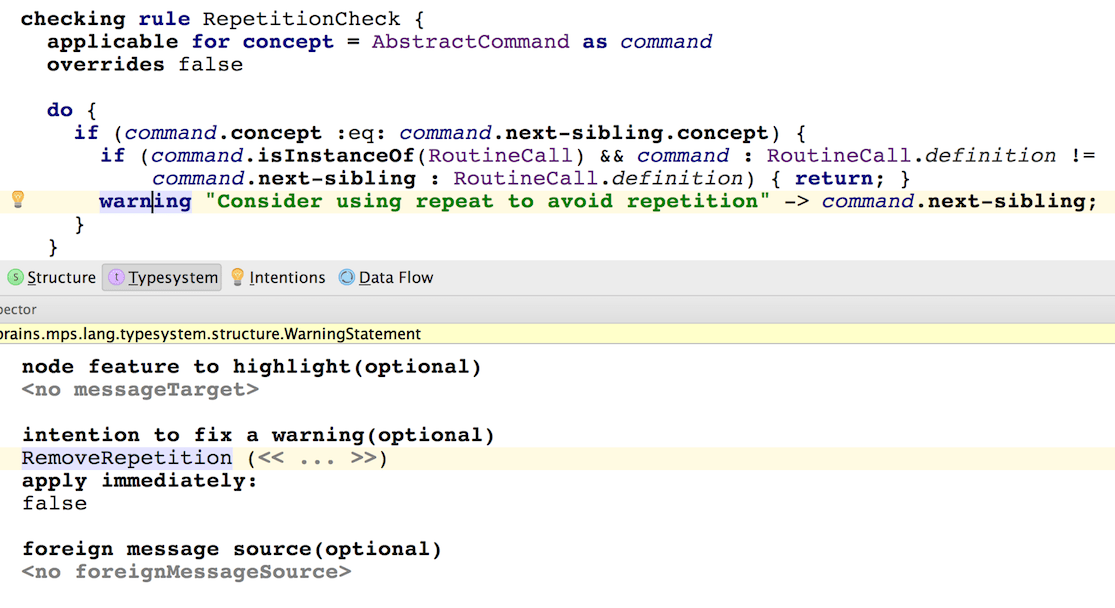
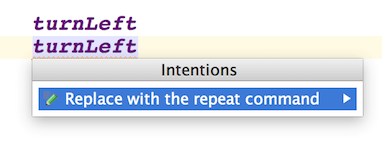
Normally the user invokes the quick-fix through the Intentions context menu, which is displayed after pressing the Alt+Enter key shortcut. If the apply immediately flag is set, however, MPS will run the associated quick-fix as soon as the problem is discovered during on-the-fly analysis without waiting for the user trigger.
The two other optional properties configured through the Inspector are needed less frequently:
node feature to highlight - specifies a node's property, child of reference to highlight as the source of the problem, instead of highlighting the whole node
foreign message source - when a user clicks (Control/Cmd + Alt + click) on the reported error in the editor, she is taken to the Checking rule's error/warning/info/ensure command that raised that error. With the foreign message source property you can override this behavior and provide your own node that the user will be taken to upon clicking on the error.
Customize the issue type
When a model-checker report is created, all issues reported by the checking rules are grouped in a single category (i.e. issue type) named "typesystem".
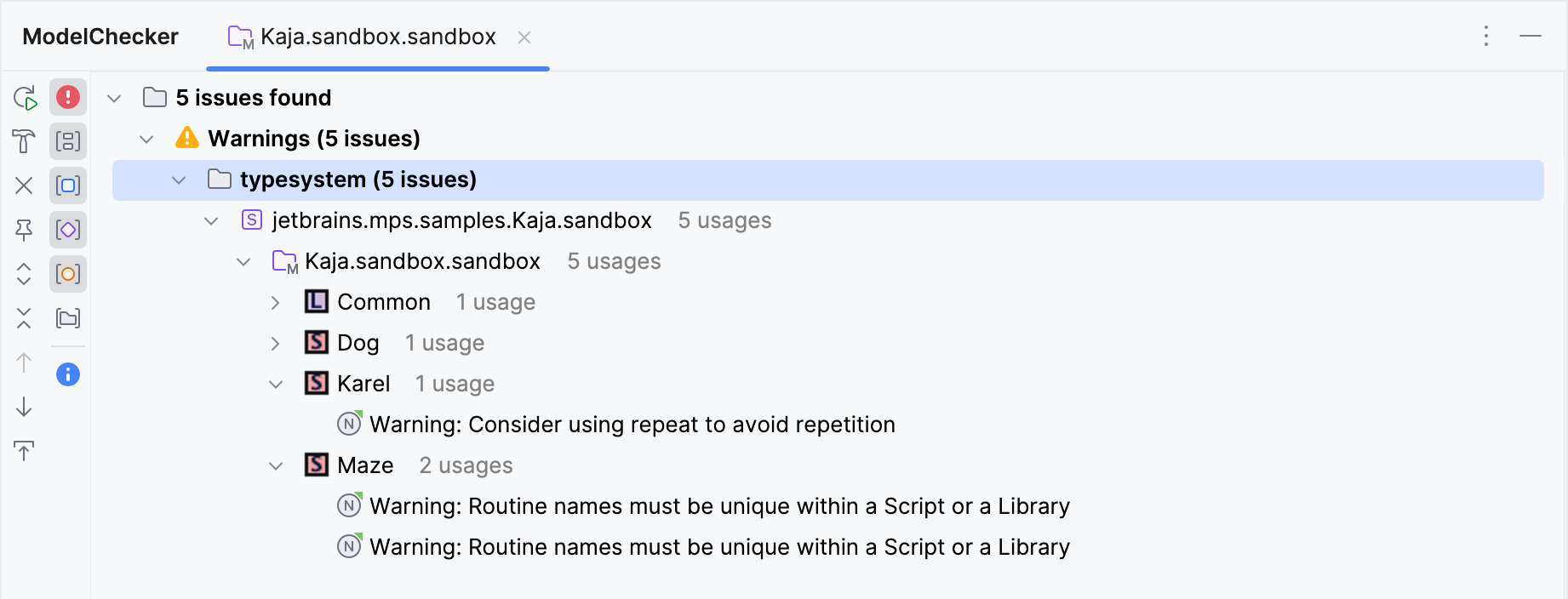
The Inspector tool allows a report statement to specify a string identifier of an issue type in which this particular issue should be included.
This allows the language designer to organize the problems in the report.
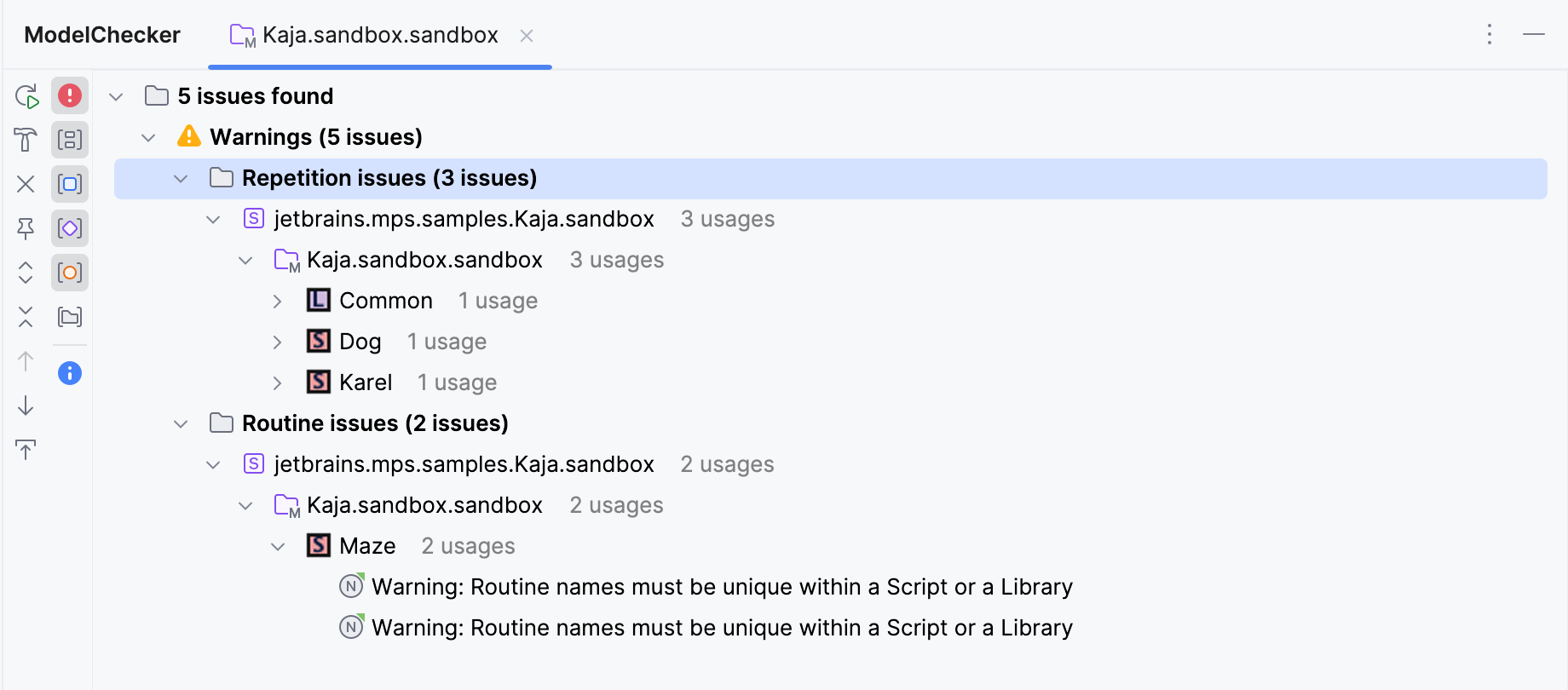
A few notes on this feature:
All report statements of the typesystem lang can have an optional issue type specified.
The issue type is defined as a string that is used to categorize issues.
The issue type can either be specified directly as a string constant or with an expression.
The users can provide their own IssueTypeSpec concept interface implementations that are generated into a string expression, which identifies the desired category.
Additional methods
The additional methods section at the bottom of inferrence rules, checking rules andd quick-fixes allows the user to define utility methods that can be called from within the corresponding root node to avoid repetition. The additional methods typically perform calculations or perform tasks that are needed in multiple places of the definition. The additional methods must be private to only be visible from within the containing node.